記号の意味
ばねの設計に用いる記号を下記の表1に示します。また、横弾性係数Gの値は表2によります。
表1. 計算に用いる記号及び単位
| 記号 | 記号の意味 | 単位 |
|---|---|---|
| d | 材料の直径 | mm |
| D | コイル中心径 | mm |
| Hf | 自由高さ | mm |
| Na | 有効巻数 | — |
| P | ばねにかかる荷重 | N |
| δ | ばねのたわみ | mm |
| k | ばね定数 | N/mm |
| Pi | 初張力 | |
| τi | 初応力 | mm |
| M | ねじりモーメント、曲げモーメント | N/mm |
| σ | 引張り応力 | N/mm2 |
| τ0 | 未修正せん断応力 | N/mm2 |
| τ | 修正せん断応力 | N/mm2 |
| κ | 応力修正係数 | — |
| c | ばね指数 | — |
| G | 横弾性係数 | N/mm2 |
| r1 | フック部曲げR | mm |
| r2 | フック部曲げR | mm |
表2.横弾性係数:G(N/m㎡)
| 材料 | Gの値 | |
|---|---|---|
| ばね鋼鋼材 硬鋼線 ピアノ線 オイルテンパー線 |
78500 | |
| ステンレス鋼 | SUS304 SUS316 SUS631J1 |
68500 68500 73500 |
| 黄銅線 | 39000 | |
| 洋白線 | 39000 | |
| リン青銅線 | 42000 | |
| ベリリウム銅線 | 44000 | |
コイル部のたわみ及び応力
コイル部のたわみの基本式は、圧縮コイルばねの式
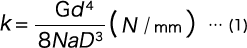
を用いて計算する。
但し、荷重については、初張力を考慮する必要があり、この初張力を Pi とすると任意荷重 P は
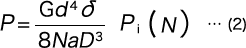
となる。式(1)よりたわみ δ は、
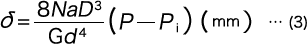
となる。また、せん断応力 τ0・τ は、圧縮コイルばねと同様に
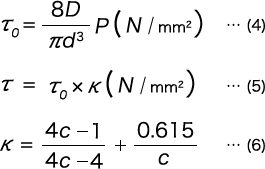
で求められる。
フック部の応力
フック部には、曲げモーメントとねじりモーメントに基づく引張応力、及びせん断応力が発生しており、正確な計算は複雑である。ここでは、広く利用されている半丸フック、Uフックについて、近似的な計算を紹介する。
(i)半丸フックの場合
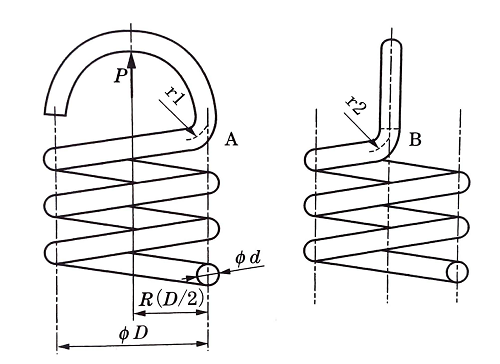
図1 半丸フック
図1において引張応力の最大値はA部の内側に、せん断応力の最大値はB部の内側に生じる。
A部内側の最大引張応力は、曲げモーメント M と軸荷重 P による引張応力との和であるから、
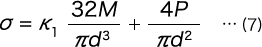
となる。ここでK1 は曲率に基づく応力集中係数で、
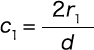 とすると次式で与えられる。
とすると次式で与えられる。
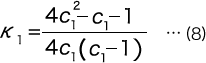
式(7)を整理すると
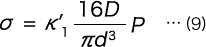
を得る。但しK1 は
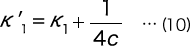
である。ここで、C はコイル部のばね指数である。
B部内側の最大せん断応力は、ねじりモーメントM によるものであり
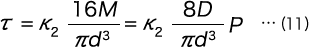
となる。ここで K2 は曲率に基づく応力集中係数で、
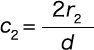 とすると次式で与えられる。
とすると次式で与えられる。
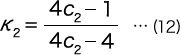
(ii)Uフックの場合
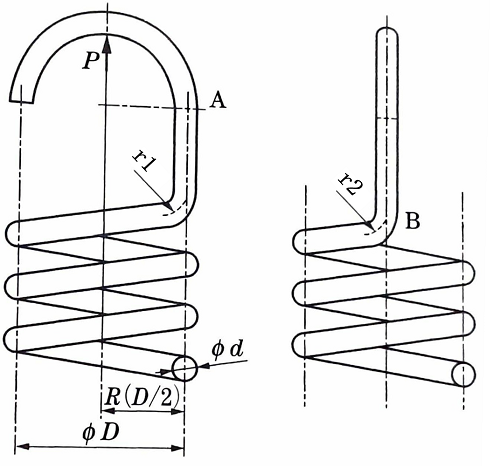
図2 Uフック
図2において引張応力の最大値はA部の内側に、せん断応力の最大値はB部の内側に生ずる。
A部内側の最大引張応力は、曲げモーメント M と軸荷重 P による引張応力との和であるから、
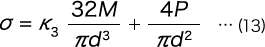
となる。ここでK3 は曲率に基づく応力集中係数で、
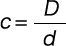 とすると次式で与えられる。
とすると次式で与えられる。
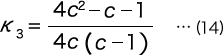
式(13)を整理すると、
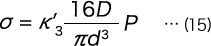
を得る。但し、K′3 は
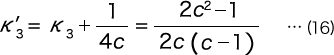
である。B部の最大せん断応力は、半丸フックと同様に式(11)で与えられる。尚、他の形状のフックについても同様に考えれば良い。






























![引きばねの導入事例[用途別]](/assets/images/products/stretch/side_2_ttl.png)