記号の意味
ばねの設計に用いる記号及び単位を表1に、縦弾性係数Eの値を表2に、
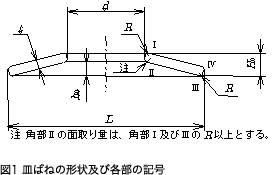
皿ばねの形状及び各部の記号を図1に示します。
表1. 計算に用いる記号及び単位
| 記号 | 記号の意味 | 単位 |
|---|---|---|
| D | 皿ばねの外径 | mm |
| d | 皿ばねの内径 | mm |
| t | 皿ばねの厚さ | mm |
| H0 | 皿ばねの自由高さ | mm |
| h0 | 皿ばねの全たわみ量(H0-t) | mm |
| E | 材料の縦弾性係数 | N/mm2 |
| v | 材料のポアソン比 | — |
| P | 皿ばねに負荷される荷重 | N |
| δ | 皿ばね単体のたわみ量 | mm |
| σI | 位置Iの応力 | N/mm2 |
| σII | 位置IIの応力 | N/mm2 |
| σIII | 位置IIIの応力 | N/mm2 |
| σIV | 位置IVの応力 | N/mm2 |
| PG | ばねを組み合わせた時の荷重 | N |
| δG | ばねを組み合わせた時のたわみ量 | mm |
| n | 並列に重ねた枚数 | 枚 |
| m | 直列に組み合わせた組数 | 段 |
| L0 | ばねを組み合わせた時の自由高さ | mm |
| R | 角部の面取り半径 | mm |
表2. 縦弾性係数:E(N/m㎡)
| 材料 | Eの値 | νの値 | |
|---|---|---|---|
| ばね鋼鋼材 | 206000 | 0.3 | |
| ステンレス鋼 | SUS302 SUS304 SUS631 |
186000 186000 196000 |
0.29 |
| リン青銅 | 98000 | 0.3 | |
| ベリリウム銅 | 127000 | ||
なお、角部IIの面取り量は、角部I及びIIIのR以上となります。
計算に用いる係数
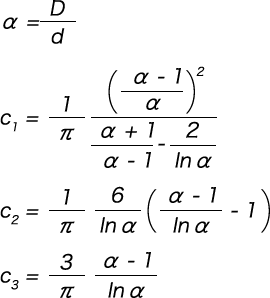
荷重の計算
荷重Pは角部のR面取りを考慮した補正項
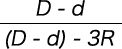 をいれ、次によります。
をいれ、次によります。
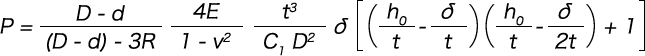
応力の計算
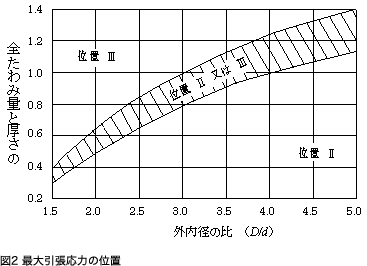
図2に示す位置I,II,III及びIVの各角部の応力を計算する。正の場合には、引張り応力であり、負の場合には、圧縮応力である。
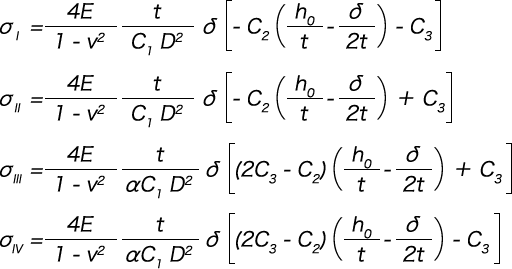
最大応力の角部発生位置
疲労寿命を検討する場合には、角部に発生する応力の内、最大応力が発生する位置で繰返し特性を検討します。皿ばねの最大応力発生位置は、外内径の比や全たわみ量と厚さの比によって異なってきます。皿ばねの最大応力発生位置は、図2に示す全たわみ量と厚さの比と外内径の比との関係に応じた位置を参考に検討を行っていきます。
皿ばねの組合せ
皿ばねは組合せ方法によって様々な荷重特性を得ることができます。
組合せ方法 ー 並列と直列
並列重ね
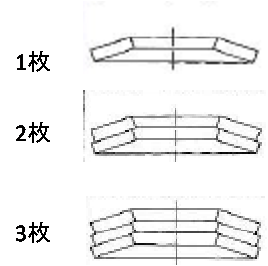
図3. 並列重ね
・荷重:大きくなる
・たわみ:変化しない
荷重:1枚当たりの荷重×並列枚数
図のように同じ向きに重ねます。
直列重ね
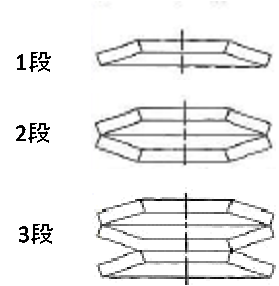
図4. 直列重ね
・荷重:変化しない
・たわみ:大きくなる
たわみ:1枚あたりのたわみ量×直列枚数
図のように互い違いに重ねます。
並列・直列組合せによる荷重・たわみの変化
図のように並列・直列の組合せに応じて、荷重及びたわみが変化します。
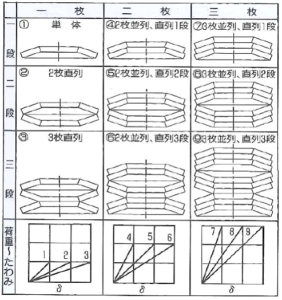
図5. 並列・直列重ねによる荷重・たわみの変化
計算値と実測値の差
実測値の荷重曲線は全たわみ量の40%までは初期ひずみ等の影響により計算値の荷重曲線より低くなり、全たわみ量の75%を超えると荷重が急激に増加します。できる限り荷重特性の安定する範囲での使用が望ましく、DIN規格では、使用最大たわみは、δ=0.75h(全たわみ量はδ=0.75h)と規定しています。
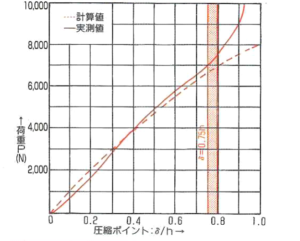
図6. 計算値と実測値の差
ガイドとクリアランス
皿ばねを組み合わせて使用する際は、内径側もしくは外径側にガイド(軸やケース等)が必要になります。ばねは圧縮により形状が変化しますので、ガイドとのクリアランスを考慮することが重要になります。
例)圧縮時の径の変化について
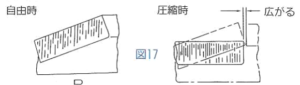
図7. 皿ばね圧縮時の径変化
圧縮するにつれ、内径は大きく、外径は小さくなる。
下の表は一般的な皿ばねのクリアランスは下記表の通りとなります。(弊社社内基準の為、JIS B 2706規格とは異なります)
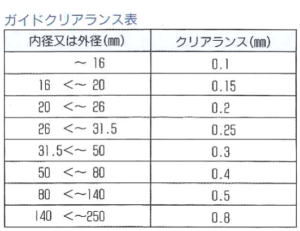
表3. 皿ばねのガイドとクリアランス
※表のクリアランスは径の片側についての値なので、実際の設計時は両端分(表記の2倍)のクリアランスが必要となります。






























![皿ばねの導入事例[用途別]](/assets/images/products/disc_top/side_2_ttl.png)