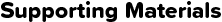Spring Design
Design information for engineers, such as spring calculation formulas,
which are the basis of spring design, can be found here.
- Tokai Spring HOME
- Spring Design
- Torsion Springs: Calculation Formulas
Torsion
Springs
Meaning of Symbols
The symbols used for spring design are shown in Table 1 below. The values of the longitudinal elastic modulus (E) are based on Table 2.
Table 1. Symbols and units used in calculations
| Symbol | Meaning | Unit |
|---|---|---|
| d | Material diameter | mm |
| Di | Coil inner diameter | mm |
| D0 | Coil outer diameter | mm |
| D | Coil average diameter D=( Di + D0)/2 | mm |
| ΔD | Reduction in coil average diameter with load applied | mm |
| N | Number of coils | — |
| v | Poisson’s ratio of materials(0.3) | — |
| c | Spring index c=D/d | — |
| E | Longitudinal elastic modulus | GpaまたはN/mm2 |
| l | Second moment of area | |
| Z | Section modulus | |
| P(P1, P2) | Load (Force) applied to the spring | N |
| M | Torsion moment (Torque) acting on the spring | N・mm |
| a1, a2 | Arm length | mm |
| L | Active extension length of the spring | mm |
| kr (krd) | Spring constant | N・mm/rad(N・mm/deg) |
| φ(φd) | Spring torsion angle | rad(deg,°) |
| R(R1, R2) | Load radius | mm |
| Ds | Guide stud diameter | mm |
| kb | Bending stress correction factor | — |
| σ | Bending stress | Gpa or N/mm2 |
Table 2.Longitudinal elastic modulus:E(N/m㎡)
| Material | E Value | |
|---|---|---|
| Spring steel material Hard steel wire Piano wire Oil-tempered wire |
206×103 | |
| Stainless steel | SUS302
SUS304(Correspond to X5CrNi18-9,1.4301,S30400) SUS631(Correspond to X7CrNiAl17-7,1.4568,S17700) |
186×103 186×103 196×103 |
| Brass Wire | 98×103 | |
| Nikel-silver wire | 108×103 | |
| Phosphor bronze wire | 98×103 | |
| Beryllium copper wire | 127×103 | |
Basic Calculation Formula Used for Design
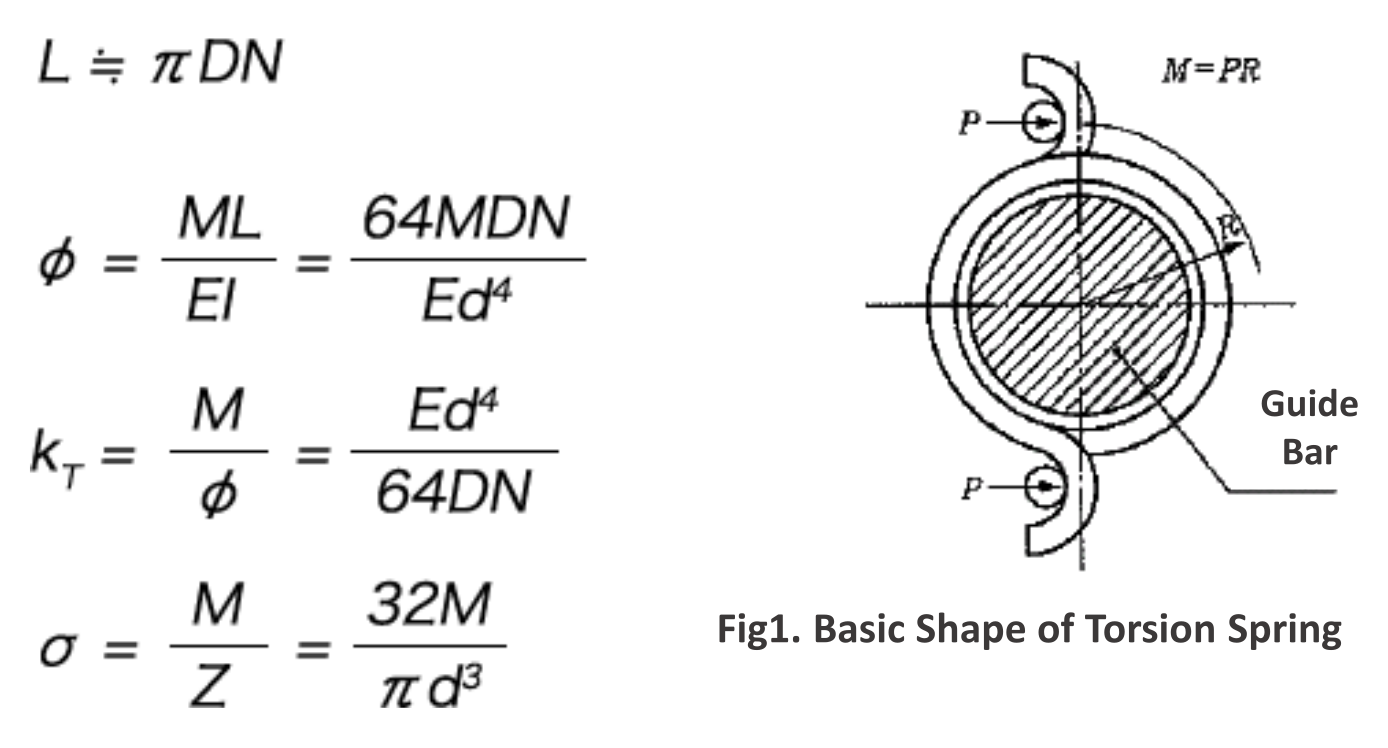
Design of Torsion Springs
The torsion coil spring must be designed in consideration of the bending deflection that occurs in the arm which extends from the coil part.
The necessity to consider the arm part can be judged with the following formula.
If a1 + a2 is 0.09π DN or more, it is recommended to consider the arm length.
![]()
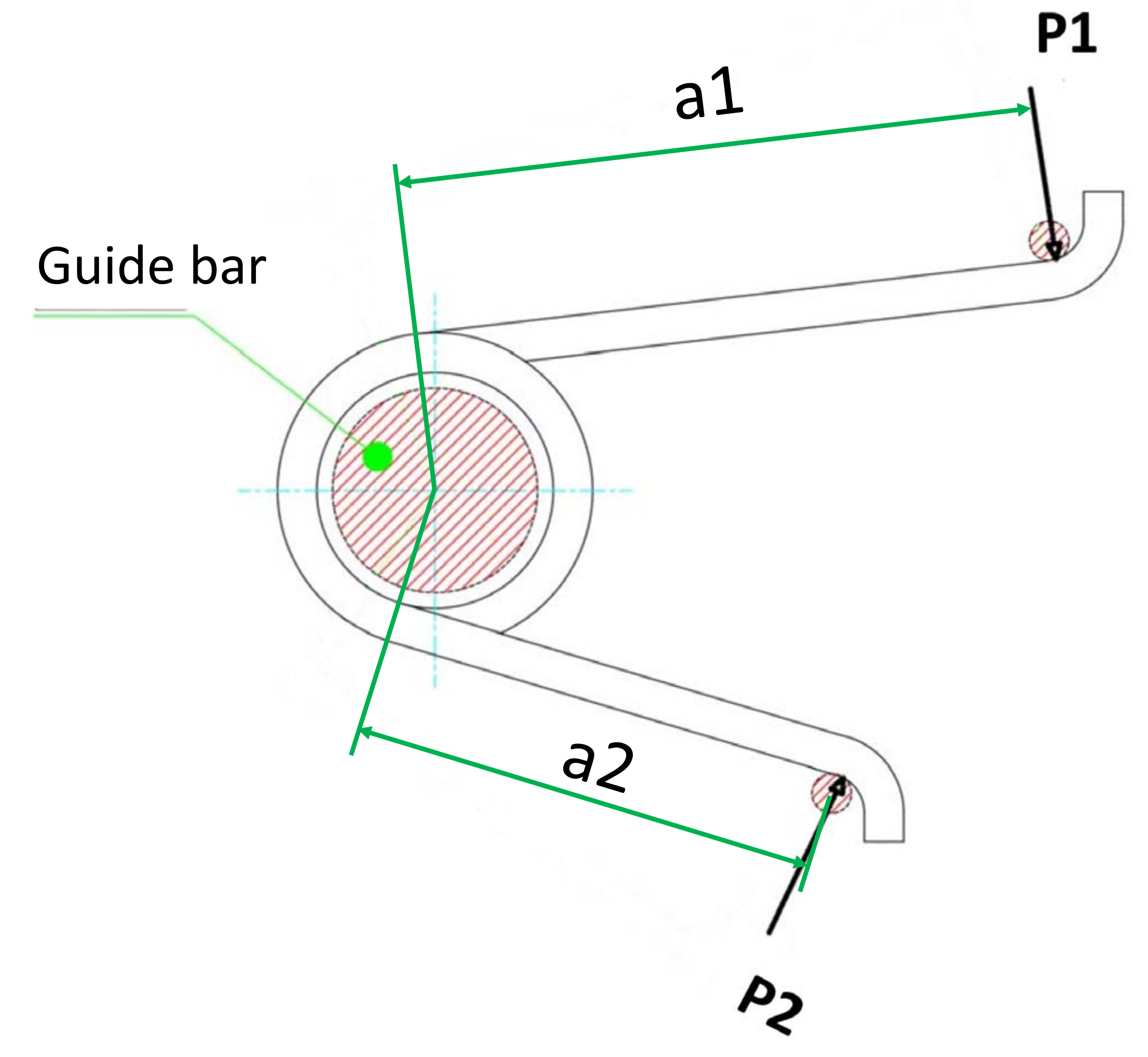
Figure 2. Arm Length of Torsion Springs
The spring constant (KT) of the torsion springs can be calculated with the following formula.
When the Length of the Arm Is Negligible

When the Length of the Arm Is Not Negligible
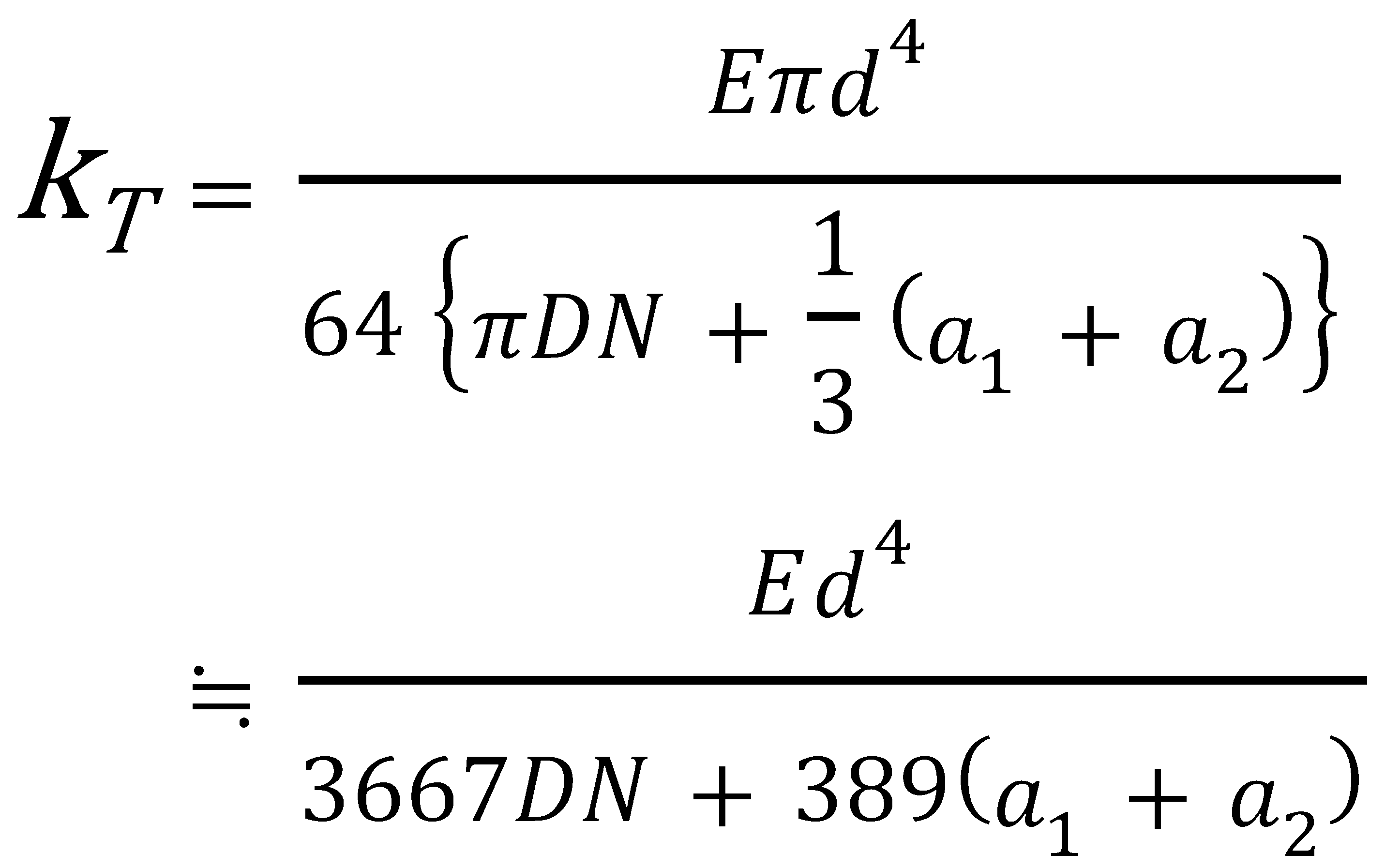
In addition, any stress (σ) can be calculated by the following formula.
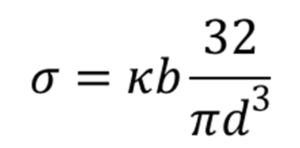
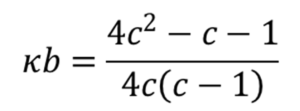
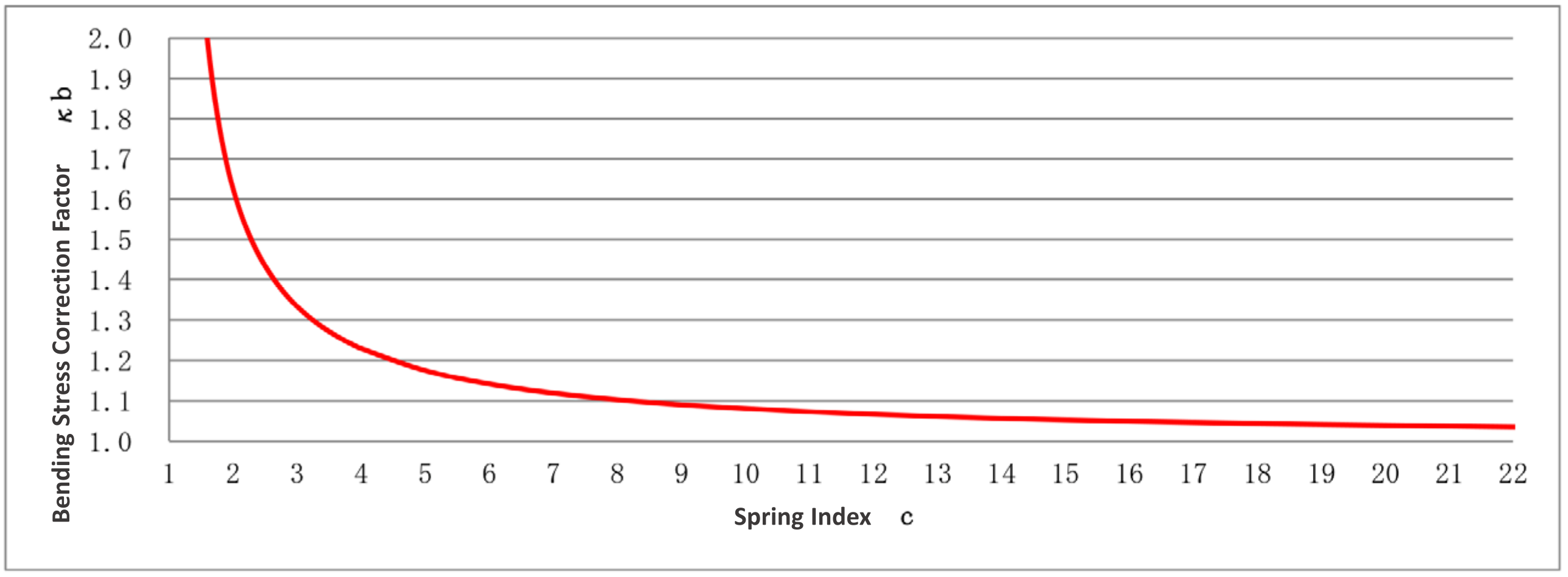
Figure 3. Relationship between Spring Index “c” and Bending Stress Correction Factor “κb”