Spring Design
Design information for engineers, such as spring calculation formulas,
which are the basis of spring design, can be found here.
- Tokai Spring HOME
- Spring Design
- Rectangular Wire Helical Springs: Calculation Formulas
Rectangular Wire
Helical Springs
Meaning of Symbols
The symbols used for spring design are shown in Table 1 below. The values of the transverse elastic modulus (G) are based on Table 2.
Table 1. Symbols and units used in calculations
| Symbol | Meaning of Symbol | Unit |
|---|---|---|
| a | Material width (perpendicular to the central axis) | mm |
| b | Material thickness (a = b for square cross-section, parallel to the central axis) | mm |
| D | Coil center diameter | mm |
| Di | Coil inner diameter | mm |
| Do | Coil outer diameter | mm |
| Nt | Total number of coils | — |
| Na | Number of active coils | — |
| Hs | Solid height | mm |
| Ｈｆ | Free length | mm |
| G | Transverse elastic modulus | N/mm2 |
| P | Load applied to the spring | N |
| δ | Spring deflection | mm |
| k | Spring constant | N/mm |
| τ | Torsional correction stress | N/mm2 |
| β | Stress calculation coefficient | |
| γ | Deflection calculation coefficient | |
| ｃ | Spring index |
Table 2. Transverse elastic modulus: G（N/mm2）
| Material | G Value | |
|---|---|---|
| Spring steel material | 7.85×104 | |
| Stainless Steel | SUS304(Correspond to X5CrNi18-9,1.4301,S30400)
SUS316(Correspond to X5CrNiMo17-12-2,1.4401,S31600) SUS631J1 |
6.85×104 6.85×104 7.35×104 |
Basic Formulas Used for Design
The basic formula for calculating the deflection at the time of compression is
calculated using
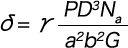
The basic formula for the spring constant is calculated by
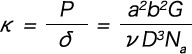
The basic formula for stress during compression is
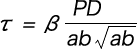The calculation coefficients β and γ differ depending on the spring index (c) and the rectangular shape. Please contact us separately for further details.
Product information
Search By Industries
