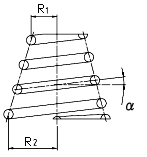
ピッチ角一定の円錐コイルばねでは、Rとｎ' (＝θ/2π）は次式で関係づけられる。
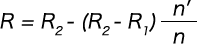したがって、無荷重時の最大コイル径から測ってｎ' 巻目までの高さＨは、ピッチ角αが小さいとき次式で表わせる。

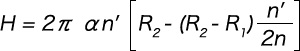
コイルが密着を始める前までのたわみは、dδ＝Rφds と dR=(ν/2πR)ds の２式から ds を消去した dδ=(2πφ/ν)R2dR を、R1から R2まで積分して求められ、
　　式（1-1）
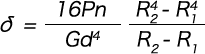
となる。最大せん断応力は最大コイル半径 R2 の点に生ずるから

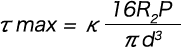
ただし、は c=2R2/d として式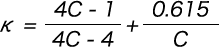から求める。
コイルが接着してからのたわみと応力は、つぎのようにして求められる。
円筒コイルばねを密着させたときのコイル展開曲線は、直線となるが、円錐ばねではある曲線をなす。
しかし横軸にθを取った接着部分の展開曲線は h=θd'/2π なる直線で表せる。
したがって実際の接着部分の展開曲線の傾斜角α' は

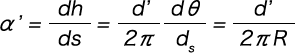
となる。ただし、ｄ' はに示す接着コイルの中心距離で次式から計算される

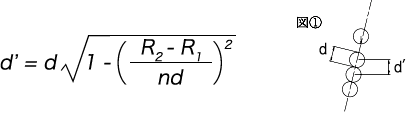
したがってピッチ角αがあまり大きくなければ、

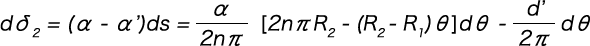
が成り立つから、これをθについて0から2ｎ2πまで積分すると

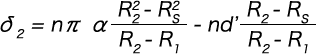
となる。ここでｎ2/ｎ＝（R2−Rs）/（R2−R1）なる関係を用いた。
δ1は式（1-1）で分子のR2のかわりにRsとおいて求められるから、結局たわみδは

　　式（1-2）

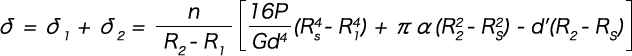
一方、荷重PはRsと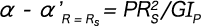

なる関係があるから、これを書きなおして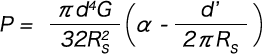
　　式（1-3）
上式をRsについて解くのは面倒であるから、荷重とたわみの関係は、Rsを媒介変数として式（1-2）、((1-3）から求めるとよい。
接着開始荷重とそのときのたわみ式は（1-2）、(1-3）でRs＝R2とおいて求められる。
円錐形の傾斜角とばねのピッチ角がともに大きければ、1−(R2−R1）/nd≦0となる場合がある。
このような場合は、コイルの密着が隣接するコイルではなく支持板に対して行われる。
この場合のたわみと荷重は式（1-2）、(1-3）でｄ'＝0とおけばよく、次式のようになる。

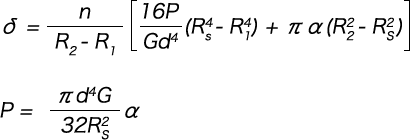
最大せん断応力τmaxは、接着が隣接コイルと座の支持面のいずれに対して行われる場合も、次式で計算される。

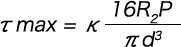
はc=2Rs/dとして、式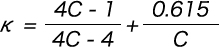から求める。


円錐コイルばね計算式（ピッチ角一定の場合）まとめ

(1) 接着開始時たわみ (2) 接着開始時応力
(3) 接着開始後たわみ ○コイル同士の接着ではなく支持板に接着場合　(1−(R2−R1）/nd≦0） (4) 接着開始後荷重 ○コイル同士が接着の場合　(1−(R2−R1）/nd＞0） ○コイル同士の接着ではなく支持板に接着場合　(1−(R2−R1）/nd≦0） (5) 接着開始後応力