記号の意味
コイルばねの設計に用いる記号を下記の表1に示します。また、横弾性係数Gの値は表2によります。
表1. 計算に用いる記号及び単位
| 記号 | 記号の意味 | 単位 |
|---|---|---|
| d | 材料の直径 | mm |
| D1 | コイル内径 | mm |
| D2 | コイル外径 | mm |
| D | コイル平均径 | mm |
| Nt | 総巻数 | — |
| Na | 有効巻数 | — |
| Hs | 密着高さ | mm |
| Hf | 自由高さ | mm |
| c=D/d | ばね指数 | — |
| G | 横弾性係数 | N/mm2 |
| P | ばねにかかる荷重 | N |
| δ | ばねのたわみ | mm |
| k | ばね定数 | N/mm |
| τ0 | ねじり応力 | N/mm2 |
| τ | ねじり修正応力 | N/mm2 |
| κ | 応力修正係数 | — |
表2.横弾性係数:G(N/m㎡)
| 材料 | Gの値 | |
|---|---|---|
| ばね鋼鋼材 硬鋼線 ピアノ線 オイルテンパー線 |
78500 | |
| ステンレス鋼 | SUS304 SUS316 SUS631J1 |
68500 68500 73500 |
| 黄銅線 | 39000 | |
| 洋白線 | 39000 | |
| リン青銅線 | C5191 | 42000 |
| ベリリウム銅線 | 44000 | |
| インコネル線 | INCONEL718 INCONELX750 |
78500 78500 |
| 合金工具鋼線 | SKD4 | 78500 |
コイルばねの設計に用いる基本計算式
コイルばねの荷重とばね定数・たわみの関係
線形特性をもつばねの荷重はたわみに比例するので
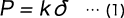
となる。
コイルばねの寸法からばね定数を求める
圧縮コイルばねにおいては、素線径にねじりがかかってタワミを生じるのでばね定数kは
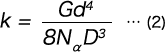
用語の説明
ばね定数とは?
ばねは、縮めたり伸ばしたりといった変形をすると元に戻ろうとする力が発生します。この力のことを弾性力と言います。弾性とは、変形をしても元に戻る現象のことです。この弾性の範囲内では変形量と力は比例の関係が成り立ちます。この弾性の範囲内で、ばねを一定の長さだけ伸縮させたときに必要な力を表したものを”ばね定数といいます。
![ばね定数 [k] の力と変形量の関係](https://www.tokaibane.com/cms/wp-content/uploads/2016/11/e_250716.jpg)
図e.ばね定数 [k] の力と変形量の関係
モータースポーツの世界ではばね定数のことを「ばねレート」や「スプリングレート」と言ったりします。英語で表すと、「spring rate」や「spring constant」となります。
ばね定数が変化する要素
ばね定数は材料径やコイル径、コイル巻数などの要素によって強くなったり弱くなります。例えば下の図f,gのように、同じばね高さ、コイル径、コイル巻数で材料径が異なる場合や、同じばね高さ、材料径、コイル巻数でコイル径が異なる場合、ばね定数が異なります。
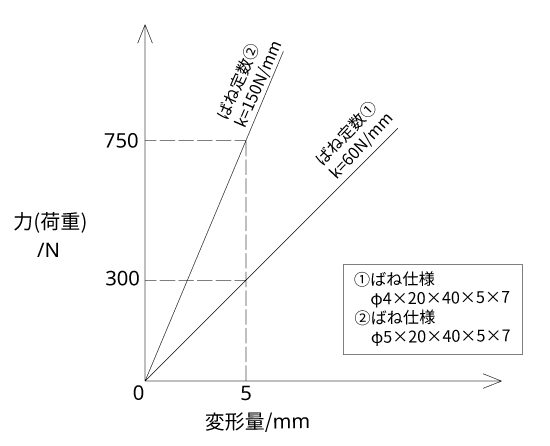
図f. 材料径の違いによるばね定数の変化
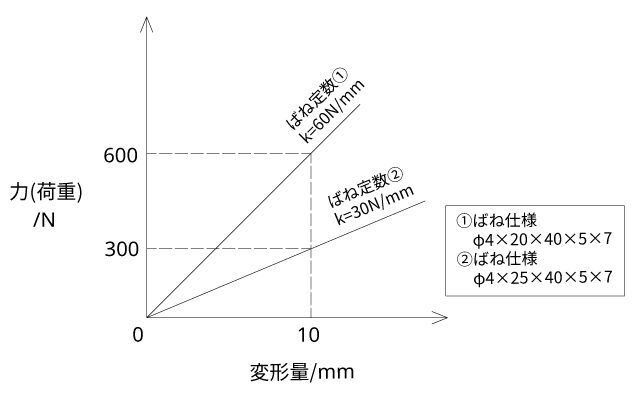
図g. コイル径の違いによるばね定数の変化
コイルばねのねじり応力
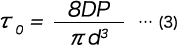
コイルばねのねじり修正応力
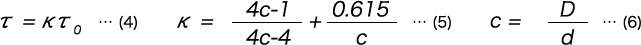
コイルばねの密着高さ(端面を研削した場合)
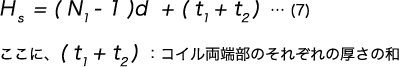
コイルばね 高温時の材質別機械的特性
表3. 温度別コイルばねの横弾性係数(N/mm2)
| 材質 | 環境 | 100℃ | 200℃ | 300℃ | 400℃ | 500℃ | 600℃ |
|---|---|---|---|---|---|---|---|
| SUP10 | 通常 | 76500 | 74300 | — | — | — | — |
| SUS304 | 耐食・高温 | 68100 | 66200 | — | — | — | — |
| SUS316 | 耐食・高温 | 68100 | 66200 | — | — | — | — |
| SKD4 | 高温 | 77000 | 74700 | 71600 | 69000 | — | — |
| INCONEL X750 | 耐食・高温 | 77700 | 76600 | 74700 | 72800 | 70900 | — |
| INCONEL 718 | 耐食・高温 | 74700 | 72400 | 70100 | 67800 | 65900 | 63600 |
表4. 温度別コイルばね許容応⼒(N/mm2)
| 材質 | 応力位置 | 100℃ | 200℃ | 300℃ | 400℃ | 500℃ | 600℃ |
|---|---|---|---|---|---|---|---|
| SUP10 | τ 0 | 490 | 410 | — | — | — | — |
| SUS304 | τ 0 | 0.7a | 0.5a | — | — | — | — |
| SUS316 | τ 0 | 0.8a | 0.6a | — | — | — | — |
| SKD4 | τ 0 | 550 | 490 | 430 | 350 | — | — |
| INCONEL X750 | τ | 482 | 482 | 482 | 482 | — | — |
| INCONEL 718 | τ | 519 | 519 | 519 | 519 | — | — |
※INCONEL材で400度以上の設計をご要望の方は こちら からお問合せください。
※「a」は、常温時の許容応力になります。
各材質における常温の許容応力は「設計応力の取り方」ページの図1を参照ください。
組み合わせのコイルばねの計算式
コイルばねの直列と並列
ばねの設計をする際、できれば、一つのばねで条件が収まるように、設計をすべきですが、
設計条件が一つのばねでどうしても満足しない場合、複数のばねを組み合わせて、設計を満たすこともあります。
ばねを組み合わせる方法としては、縦に重ねていく直列法と横に並べていく並列法の二つのパターンがあります。
このような分類は、コイルばねだけに関わらず、皿ばねやその他の種類のばねでもあり、同等に、
直列や並列の組み合わせで使用します。荷重の観点から考えると、各ばねに作用する力が等しいような組み合わせ方を直列と言い、
各ばねの変位が等しくなるような組み合わせ方を並列と呼んでいます。
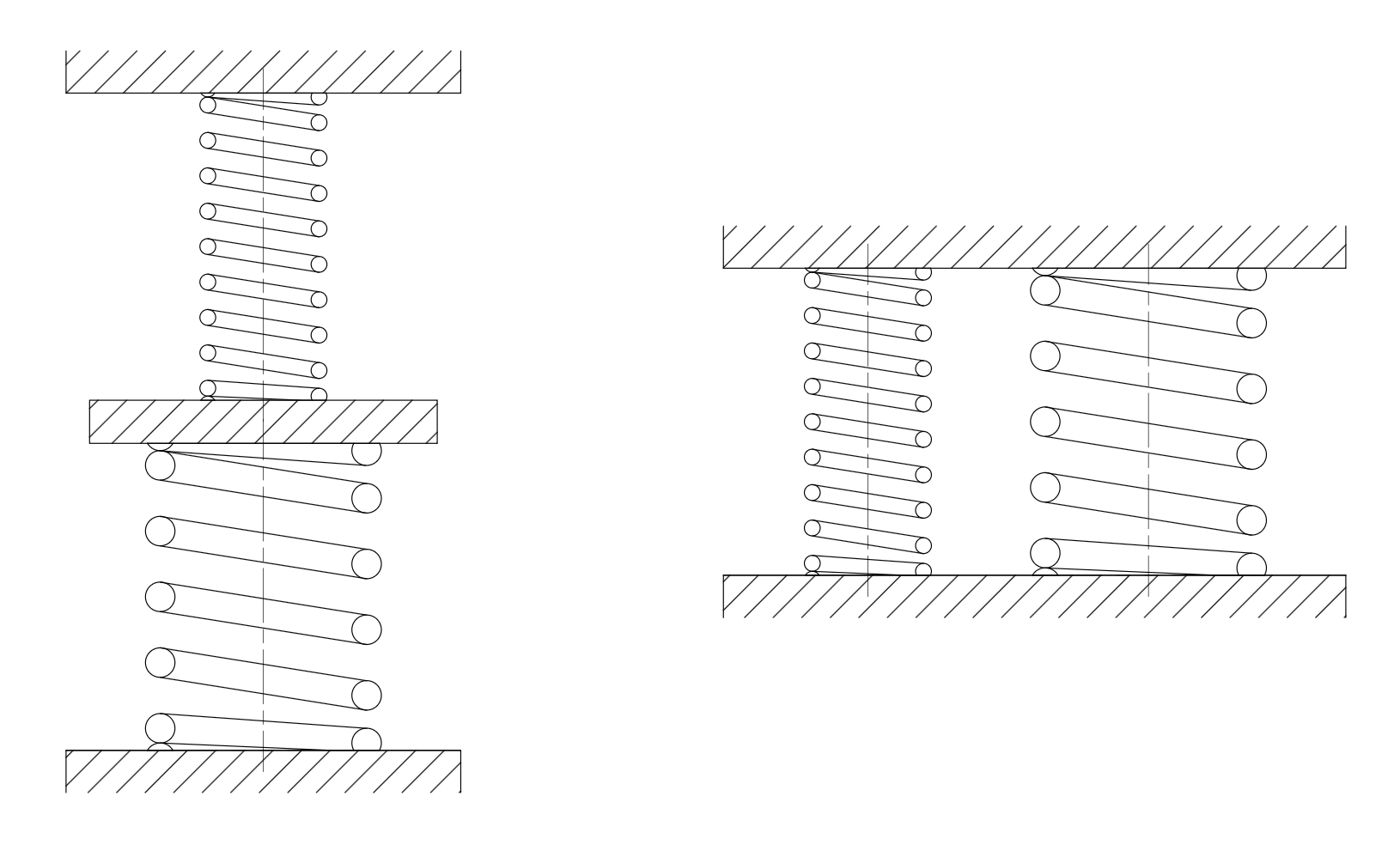
図1. コイルばねの直列組合せと並列組合せ
3個のコイルばねを使用する場合の例を取って図示しました。
n個のばねのそれぞれのばね定数を k1 , k2 ,・・・, kn
とした時、それらのばねを並列と直列組み合わせた時の全体のばね定数Kは次式で与えられます。
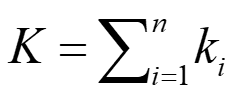
式1. 並列のばね定数計算式
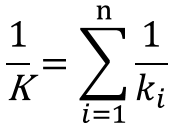
式2. 直列のばね定数計算式
並列では、コイルばねの個数が増える程全体のばね定数が大きくなっていくのに対して、直列では個数が増えるほど全体のばね定数は小さくなります。
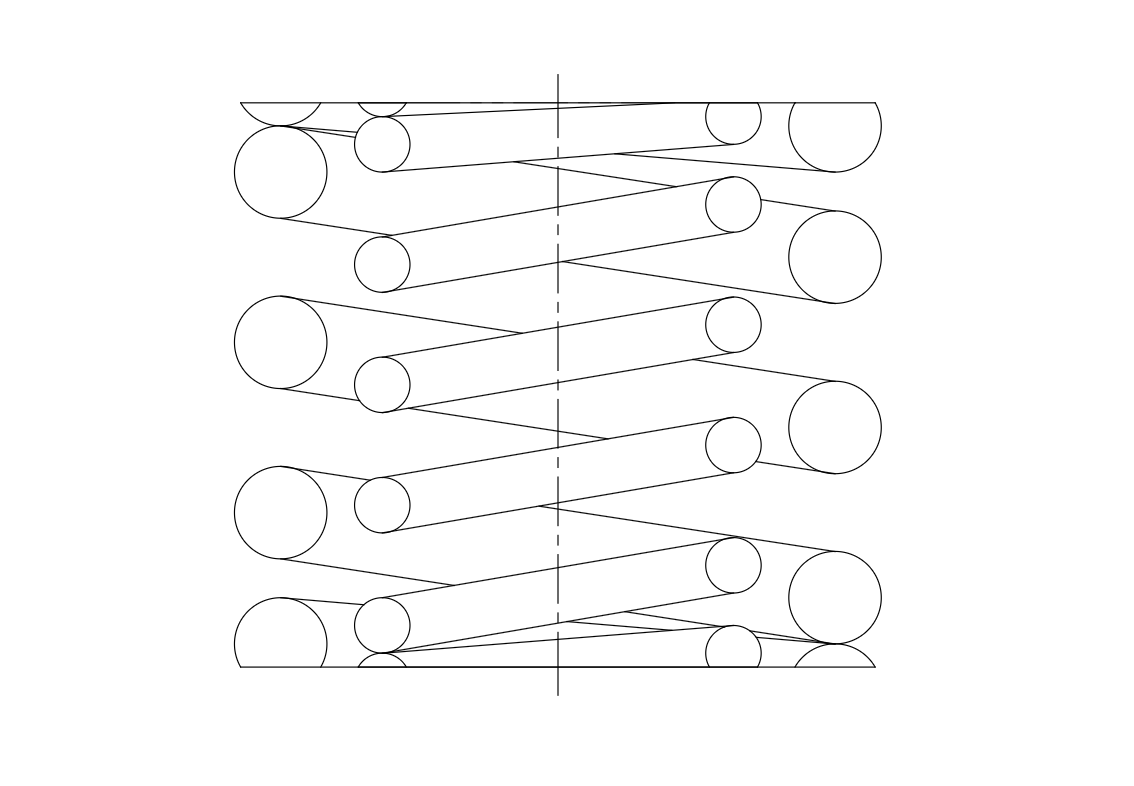
図2. 親子ばね
並列は横並びにすると言いましたが、単に横に並べていくとスペースを取ってしまうので、図2のようにばねの内側にばねを組み合わせ、同心に並べることが多いです。これをその姿から親子ばねと呼ぶこともあります。
ただし、同心の組み合わせの場合には、ばねどうしが絡み合わないように、交互に巻方向を変えたり、ばねとばねの間に一定の隙間を確保する必要があります。
また、ばねの組合わせ方を工夫すると、下図3,4のように、直線でないばね特性を作ることができます。
たとえば図3のようなばね特性が必要な場合は、自由長または密着荷重の違うばねを直列に組み合わせる必要があります。
図4のばね特性は図5のような機構の中にばねを入れ、〔上段のばね定数〕<〔下段のばね定数〕という組み合わせをつくると得られます。
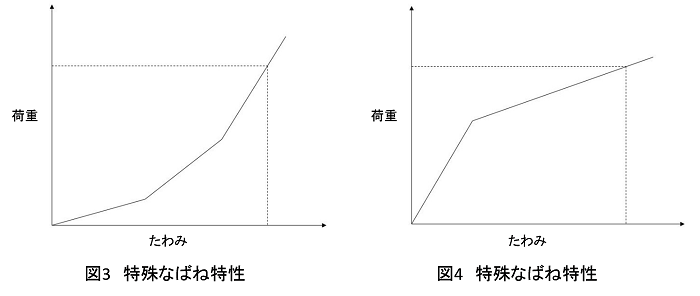
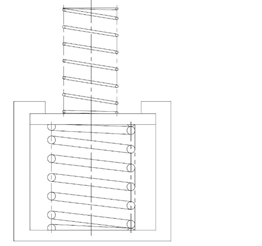
図5. 特殊なばね特性を得る機構
弾性エネルギーの計算式
ばねに蓄積されるエネルギー
ばねに荷重が加わると、そのエネルギーがばねに蓄積されていく。
ばねが蓄積するエネルギーUは、図6における荷重P―変位δ曲線で囲まれる面積に相当し、
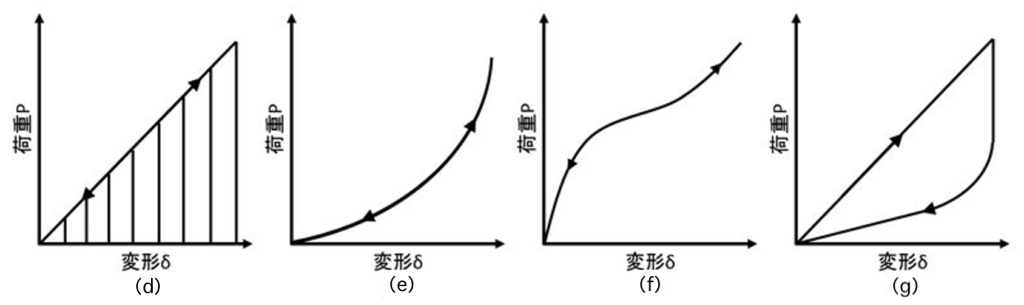
図6. ばねに蓄積されるエネルギー
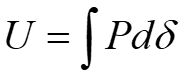
式3
で表される。 一般的に知られているばね蓄積エネルギー式である。
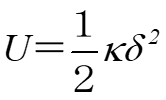
式4
は上図(d)のように両者に線形関係がある場合。つまり
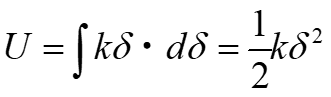
式5
となる場合だけである。
また、エネルギーの蓄積と開放について述べると、一般的には、図6の(d),(e),(f)に示すように、
荷重を加えていく時と荷重を除いていく時では、同じ荷重―変位曲線(直線)を通るので、
荷重を加えて蓄積されたエネルギーは荷重を取り除く過程で全て開放されるが、
図6(g)のようなヒステリシスループを持つばね特性の場合には、ループで囲まれている面積分のエネルギーが
荷重を加えてから取り除くまでの1サイクルで消費される。
コイルばね ばね振動の計算式
コイルばねには固有の振動数がある
ばねに荷重を加えたり、変形させたり、力を加え、その力を取り除くとばねは振動するが、その振動数はばねによって違い、それぞれ固有の振動数をもっています。
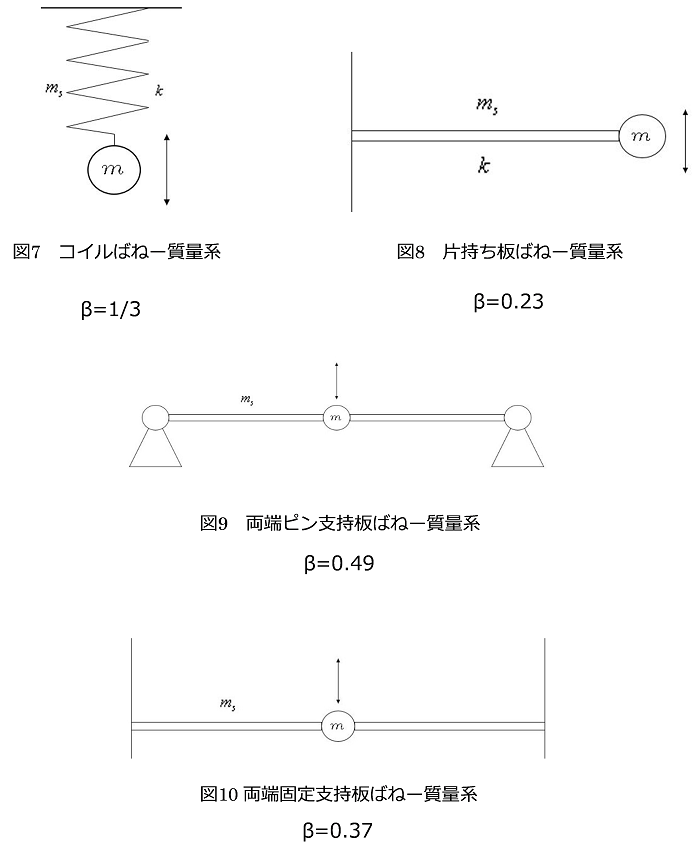
ばね自体の質量を ms とした時、その固有振動数 f は
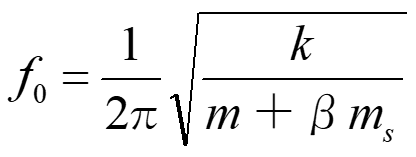
式6
と表せます。 ここで α
は、ばねを固定する条件と振動の方向によって定まる定数となります。
※例えば両端自由または両端固定のコイルばねでは、α=i/2、一端固定他端自由のコイルばねでは、α=(2i-1)/4、ここにi=1、2、・・・(整数)
また図7,8,9,10に示すように質量 ms のばねで質量 mの物体を固定し、物体を振動させた時の固有振動数 f0 は
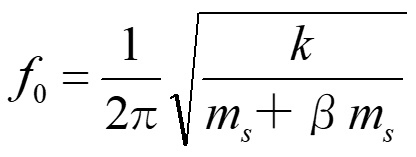
式7
で表すことができます。(ここでは板ばねの場合も合わせて説明します。)
ばねの質量 ms は物体の質量 mに比べ小さいことが多いので一般的にβ=0と見なすことが多いですが、
ばねの質量を考えなければならない時は、近似的に図9でβ=0.49、図10でβ=0.37として計算します。
ばねを設計する場合には、ばね定数はもちろん大切ですが、この固有振動数も考慮しなければならないことが多くあります。
ばね衝突の計算式
衝撃緩和こそばねの出番
衝突時の衝撃をやわらげるために、効果的な手段としてばねを用いることがあります。
衝突をやわらげる能力を評価する基準として、次のように緩衝効率 ηが定義されています。
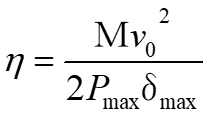
式8
ここで M は衝突する側の質量、v0 は衝突する速度、Pmax が最大衝突力、δmax は衝突された側の最変位としています。 ηの値は0以上1以下であり、理想的な場合、1となりますが、ばね定数が一定のばねの衝突効率 η は1/2となります。






























![コイルばねの導入事例[用途別]](/assets/images/products/big_coil/side_2_ttl.png)